Investigación - Departamento de Matemática

Página en construcción

El Departamento cuenta con investigadores o grupos en los siguientes temas

Geometría Diferencial y Grupos de Lie

El grupo de Geometría Diferencial y Teoría de Lie de Rosario se forma alrededor del año 2006. Al día de hoy cuenta con siete integrantes, de los cuales seis son docentes investigadores y uno es doctorando. En estos años se han desarrollado, en el marco del grupo, cinco tesinas de grado y cuatro tesis de doctorado. Los integrantes participan continuamente de jornadas científicas del área así como de carácter general, presentando trabajos en las Reuniones Anuales de la Unión Matemática Argentina, la Escuela de Geometría Diferencial (tanto la realizada periódicamente en Argentina como en Brasil), el Congreso Internacional de Matemáticos (ICM) así como de numerosos eventos de temáticas específicas. Cuenta además con numerosas publicaciones en revistas de prestigio internacional. Se realizan trabajos de investigación en temas de Geometría Riemanniana y Pseudo Riemanniana, Teoría de subvariedades, espacios homogéneos y simétricos, análisis en grupos de Lie, análisis armónico en grupos de Lie y aplicaciones a EDP. Integrantes: Isolda Cardoso, Viviana del Barco, Pablo Montenegro, Gabriela Ovando, Silvio Reggiani, Mauro Subils y Francisco Vittone.

Más información en la página del grupo.

Optimización Combinatoria: Teoría, Algoritmos y aplicaciones

Numerosos y diversos problemas de optimización de recursos, ligados a situaciones reales, pueden ser formulados como problemas de Optimización Combinatoria. La mayoría de ellos son problemas muy complejos de resolver, pertenecientes a la clase de problemas NP-difíciles. Sin embargo, la necesidad práctica de su resolución en forma exacta o aproximada ha dado un gran impulso al estudio estructural de los mismos. En este sentido, desde el punto de vista teórico, el enfoque poliedral y la teoría de grafos han aportado en forma similar en la descripción estructural de los problemas y la resolución de conjeturas del área. En términos prácticos, estos estudios han contribuido al diseño y mejora de algoritmos específicos.

Los desarrollos de este grupo se enmarcan en el estudio teórico estructural de diferentes problemas de Optimización Combinatoria y su aplicación al desarrollo de algoritmos para su resolución.

Investigadores de la FCEIA en el área: Graciela Nasini, Mariana Escalante, Daniel Severin, Paola Tolomei, Patricia Dobson, Valeria Leoni, Ma. Inés López Pujato, Yanina Lucarini, Érica Hinrichsen, María Elisa Ugarte, Pablo Fekete, Pablo Torres

Estudiantes de doctorado: Natalí Vansteenkiste, Ma. Gracia Cornet, Lara Fernández, Mauro Lucci.

Estudiantes de grado: Leandro Del Río (becario CIN), Lucía Moroni, Victoria Kaial.

Cálculo fraccionario

El cálculo fraccionario se remonta a fines del siglo XVII. Por tres siglos esta teoría fue extendida como un campo de la matemática pura. En los últimos años han sido desarrollados numerosos trabajos en este campo. Esto se debe fundamentalmente, por un lado, a que las ecuaciones diferenciales fraccionarias establecen modelos muy superiores a los que utilizan ecuaciones diferenciales con derivadas enteras porque incorporan al modelo cuestiones de memoria o efectos posteriores que se desprecian en los modelos con derivada clásica. Por otro lado, estas nuevas teorías sobre el cálculo fraccionario, juegan un rol muy importante y en creciente desarrollo en dominios muy variados como la economía, la probabilidad, como así también en la física. Esto ha originado un importante crecimiento de su estudio en las últimas décadas.

Este grupo se dedica a abordar varios enfoques:

extender la teoría de optimización y del control óptimo utilizando ecuaciones diferenciales en derivadas fraccionarias (problemas de optimización y control óptimo fraccionarios, métodos numéricos),
desarrollo de modelos inteligentes que aprenden de los datos (deep learning) utilizando gradientes fraccionarios,
estudio de modelos de orden fraccionario relacionados a células infectadas con HIV en tratamiento (análisis de estabilidad, análisis numérico)

Integrantes del grupo: Eduardo Santillan Marcus, Gabriela Reyero, Ariel Lombardi, Mariela Olguin, Melani Barrios, Alberto Ferrari, Maximiliano Mecoli, Sofía Leegstra, Daiana Bravo.

Análisis Numérico de Ecuaciones Diferenciales

Las ecuaciones diferenciales parciales constituyen la base de muchos modelos matemáticos de fenómenos físicos, químicos y biológicos y más recientemente su uso también se extiende a economía, pronósticos financieros, procesamiento de imágenes entre otros campos. Para investigar las predicciones de tales modelos, en general es necesario aproximar sus soluciones numéricamente. Muchos métodos numéricos están disponibles: diferencias finitas, elementos finitos, métodos espectrales, de colocación, probabilísticos, de partículas, para nombrar algunos pocos.

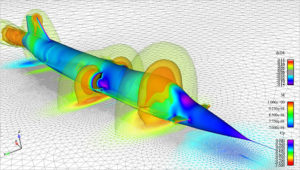
Nosotros nos concentramos en métodos de elementos finitos, que se caracteriza por la discretizacion del dominio computacional mediante mallas, que son particiones poligonales del dominio, y la construcción de espacios de funciones aproximantes que, restringidas a cada elemento de la malla, contienen un espacio de polinomios de grado dado. Las ventajas de método reside en la flexibilidad para tratar con dominios complicados y de producir espacios aproximamente de distintos grados de suavidad, y por su sólida fundamentación teórica basada en el Análisis Funcional y en la teoría de Ecuaciones Diferenciales.

Algunos de los tópicos que consideramos son:

Problemas de convección difusión: aproximación de capas límites.
Mallas anisotrópicas y diseño de mallas adaptadas a singularidades. Estimaciones de error de interpolación.
Ecuaciones elípticas en poliedros con singularidades en vértices y aristas.
Ecuaciones elípticas en dominios con cúspides.

Más información y artículos publicados pueden encontrarse en esta página personal

Teoría de juegos, diseño de mecanismos y aplicaciones

Las teorías de tomas de decisiones en situaciones dinámicas, en particular la de Control Óptimo y la de Juegos Dinámicos, que son objeto de estudio de nuestro grupo, son herramientas fundamentales en el modelado y análisis lógico y matemático de situaciones en donde los escenarios son influenciados por situaciones externas, o bien por interacciones de conflicto o cooperación. Cuando las técnicas y desarrollos obtenidos de manera teórica provenientes de estas áreas se aplican a problemas concretos, se obtienen resultados que pueden ser o no los deseables a nivel social, económico y/o político. La consideración de un “planificador” o ente regulador introduce la aparición de Diseños de Mecanismos, ocupados de pergeñar instancias de problemas cuyos resultados busquen alcanzar determinados objetivos.
Entre las aplicaciones del Diseño de Mecanismos se encuentran disciplinas muy diversas, atrayendo nuestro interés particular, la gestión del transporte urbano en grandes aglomerados, el problema de mitigar la contaminación producto del desarrollo de la actividad económica, y más en general, entre aquéllos provenientes de la gestión de recursos naturales, los abocados a garantizar Economías Sostenibles y Sustentables. La economía sostenible es aquella en donde se integran y equilibran elementos sociales, ambientales y económicos. Este modelo persigue el cuidado del medio ambiente, acompañando el proceso de mejora y aumento de bienestar de la sociedad que contiene. Se busca mantener un equilibrio a través del uso inteligente de los recursos y evitar el impacto antrópico a corto, mediano y largo plazo.

Alguna de las actividades que desarrollamos son:

estudio de la teoría de juegos y del diseño de mecanismos,
estudio de equilibrios que consideren la aversión al riesgo,
diseño de modelos estocásticos de decisión con tazas de actualización no constantes y horizonte infinito, para agentes con aversión (o preferencia) a situaciones de riesgo,
análisis y modelado de problemas donde intervenga un planificador con el objetivo de optimizar un criterio social,
implementaciones numéricas de los modelos analizados.

Integrantes: Dra. María Evangelina Alvarez, Sr. Rolando Javier Cardozo, Dr. Eugenio Martín Della Vecchia, Sra. Azul Giovagnoli, Dra. Elina Mafalda Mancinelli, Dra. Jorgelina Walpen.

Proyectos de Investigación del DM

Análisis Variacional Estocástico (UNR)
Dirección: Dr. Lisandro Parente
Codirección: Dra. Justina Gianatti
Integrantes: Lic. Emelin Buscaglia
Resumen: El proyecto está abocado al estudio de problemas con componentes estocásticas en el campo del análisis variacional. Se abordan dos líneas de trabajo: por un lado problemas de control óptimo estocástico en donde interviene la ecuación de Fokker-Plank (en particular Juegos a Campo Medio), por el otro, inecuaciones variacionales estocásticas de naturaleza dinámica. Se diseñan esquemas de aproximación numérica (analizando consistencia, estabilidad, propiedades de convergencia) y se realizan implementaciones computacionales en problemas específicos.

Problemas de optimización, control óptimo y equilibrio sobre redes. Aplicaciones a transporte, tráfico, energía y modelos epidemiológicos (PIP)
Dirección: Dr. Pablo Lotito
Codirección: Dr. Lisandro Parente
Integrantes: Dra. Laura Aragone, Dra. Justina Gianatti, Lic. Emelin Buscaglia, Lic. Jerónimo Neder.
Resumen: Este proyecto aborda dos líneas bien definidas enmarcadas en el análisis variacional de ecuaciones generalizadas y la incorporación de elementos estocásticos. Desde el punto de vista práctico se trata de distintas instancias de problemas de optimización sobre redes. Abordaremos, el diseño óptimo de redes y la calibración de parámetros en modelos de tráfico, transporte público, demanda eléctrica y la estimación de matrices de movilidad para modelos de transmisión de enfermedades, haciendo hincapié en la eficiencia computacional.
Herramientas para gestión eficiente de la generación renovable y distribuida de la energía (PICT)
Dirección: Dr. Pablo Lotito
Codirección: Dr. Lisandro Parente
Integrantes: Dra. Laura Aragone, Dra. Justina Gianatti, Lic. Emelin Buscaglia.
Resumen: Este proyecto busca contribuir a aumentar la capacidad y la eficiencia en la producción y el consumo de energía eléctrica a partir de fuentes renovables, desarrollando herramientas que asistan a la gestión de la generación distribuida y a la operación de las redes de distribución.
Control y Optimización. Teoría y Aplicaciones (UNR)
Dirección: Dra. Laura Aragone.
Codirección: Dr. Lisandro Parente
Integrantes: Dr. Santiago Muro, Dra. Justina Gianatti, Lic. Emelin Buscaglia, Lic. Jerónimo Neder.
Resumen: En este proyecto se realiza el análisis tanto desde el punto de vista teórico (existencia, unicidad, regularidad, estabilidad y comportamiento asintótico de soluciones) como numérico (soluciones aproximadas, convergencia, acotación del error), de diversos problemas de Análisis Variacional asociados a los siguientes temas: problemas binivel, problemas de control óptimo en el marco determinístico y estocástico, optimización no diferenciable, sistemas dinámicos asociados a operadores, operadores en espacios semi-Hilbertianos y aplicaciones.
Abordajes teóricos y prácticos de problemas de optimización combinatoria y sus aplicaciones (PIP).
Dirección: Dra. Graciela Nasini
Integrantes: Dr. Pablo Torres, Dr. Daniel Severín, Dra. Yanina Lucarini, Lic. María Gracia Cornet, Lic. Mauro Lucci, Lic. Natalí Vansteenkiste.
Resumen: El presente proyecto incluye las tareas de parte del grupo de investigación Optimización Combinatoria de la UNR desde donde se abordan una gran variedad de problemas del área, analizando aspectos de complejidad computacional, diseño de algoritmos aplicaciones a situaciones reales, integrando aportes de la teoría de grafos con las herramientas informáticas específicas de resolución.
Análisis de la complejidad computacional de problemas de optimización combinatoria y diseño de algoritmos para su resolución (PICT).
Dirección: Dra. Graciela Nasini
Integrantes: Dra. M. Escalante, Dra. V. Leoni, Dr. P. Torres, Dra. P. Tolomei, Dr. D. Severín, Dra. M. P. Dobson, Dra. E. Hinrichsen, Dra. M. I. López Pujato, Dra. Y. Lucarini, Dra. M. Ugarte, Lic. M. G. Cornet, Lic. M. Lucci, Lic. N. Vansteenkiste, Lic. L. Fernández.
Resumen: En este proyecto se trabaja en la complejidad computacional y el diseño de algoritmos para diferentes problemas de Optimización Combinatoria, utilizando las herramientas que aportan la teoría poliedral y la teoría de grafos. En particular, se trabajará en los siguientes tópicos: 1) Variaciones de los Problemas de Empaquetamiento y Dominación en Grafos, 2) Algoritmos de resolución de problemas provenientes de aplicaciones.
Variaciones del Problema de Dominación y Empaquetamiento Generalizado en grafos (UNR)
Dirección: Dr. Pablo Torres
Integrantes: Dra. G. Nasini, Dra. V. Leoni, Lic. M. G. Cornet, Lic. N. Vansteenkiste, Est. Leandro del Río.
Resumen: El presente plan incluye las tareas de parte del grupo de investigación Optimización Combinatoria de la Universidad Nacional de Rosario desde donde se abordan una gran variedad de problemas del área, estudiando aspectos de Teoría de Grafos y Complejidad Computacional de problemas. Los temas específicos que aborda este plan han sido clasificados en dos líneas de investigación: Variaciones del Problema de Dominación en grafos y Problema de empaquetamiento generalizado en grafos. A su vez, el primero de ellos se divide en dos subtemas: Parámetros de dominación en grafos de Kneser y Problema de Dominación Romana y sus variantes en grafos.
Problemas de optimización combinatoria: análisis de estructuras en grafos, estudio poliedral y diseño de algoritmos (UNR).
Dirección: Dra. Mariana Escalante
Integrantes: Dra. M. Ugarte, Dra. V. Leoni, Dr. P. Fekete, Dra. P. Tolomei, Dra. E. Hinrichsen, Dra. M. I. López Pujato, Dra. Y. Lucarini, Est. L. Moroni, Est. V. Kaial.
Resumen: En el presente proyecto abordamos dos grandes familias de problemas combinatorios (Coloreo en grafos y Variaciones del problema de dominación en grafos) donde utilizamos: búsqueda de facetas de los poliedros región factible de las relajaciones lineales, asociadas a estructuras en un grafo relacionado. A su vez estas facetas pueden ser utilizadas en algoritmos de plano de corte para hallar cotas para la función objetivo de los respectivos problemas. Se proponen los siguientes cinco subtemas de investigación: Problema de mínima violación cromática, Propiedad de persistencia en formulaciones del problema de coloreo, $k$-upla dominación de grafos arco-circulares, Estudio poliedral de $M$-dominación en grafo, Secuencias de dominación de máxima cardinalidad.
Algoritmos eficientes para problemas de dominación y empaquetamientos en grafos (UNR)
Dirección: Dra. Valeria Leoni
Integrantes: Dra. M. P. Dobson, Dra. Érica Hinrichsen, Dra. María Inés López Pujato, Lic. Vanesa Vansteenkiste.
Resumen: Es nuestro interés seguir modelando a través de grafos, problemas reales de ubicación de servicios que se traducen en la introducción de nuevas restricciones al problema de empaquetamiento limitado (PEL). Más específicamente, propondremos variaciones del problema tradicional, que tienen que ver con el cumplimiento de restricciones de «igualdad» en el número de elementos a ubicar dentro de la vecindad de cada usuario. Se pretende también modelar y comenzar el estudio de variante del PEL en la que las vecindades de cada posible ubicación del servicio sean abiertas. Se pretende avanzar sobre el problema abierto de decidir si hay una equivalencia polinómica general entre k-DOM y k-LP o, por el contrario, si existe una clase de grafos donde uno de los problemas es P y el otro NP-c. La misma pregunta puede ser formulada para la relación entre la complejidad computacional de {k}-DOM y {k}-PF y entre k-LP y {k}-PF.
Equilibrios multiagente, diseño de juegos y aplicaciones (UNR)
Dirección: Dra. Elina Mancinelli.
Codirección: Dra. María Evangelina Alvarez.
Integrantes: Dr. Eugenio Della Vecchia, Dra. Jorgelina Walpen, Est. Azul Giovagnoli, Est. Rolando Javier Cardozo.
Resumen: En este proyecto se realizan análisis tanto desde el punto de vista teórico (existencia, unicidad, regularidad, estabilidad de soluciones) como numérico (implementación de algoritmos de simulación y resolución, calibración de modelos). El objetivo es el desarrollo de modelos matemáticos, algoritmos y herramientas informáticas para resolver problemas ligados a la evaluación, planificación, explotación y gestión de redes y a la gestión de recursos.
Análisis y modelado a través de diseño de mecanismos de problemas donde intervenga un planificador con el objetivo de optimizar un criterio social (disminución de la congestión y la polución, eficiencia y reducción de subsidios al transporte público, sustentabilidad, preservación del medio ambiente, etc.). Estudio de equilibrios que consideren la aversión al riesgo de los agentes.
Análisis Numérico de Ecuaciones Diferenciales Parciales: Elementos Finitos y Métodos Relacionados (UNR)
Dirección: Dr. Ariel Lombardi.
Codirección: Dra. María Evangelina Alvarez
Integrantes: Dra. Melani Barrios, Lic. Cecilia Penessi, Est. José Digrazia.
Resumen: Nos concentramos en métodos de elementos finitos, que se caracteriza por la discretizacion del dominio computacional mediante mallas, que son particiones poligonales del dominio, y la construcción de espacios de funciones aproximantes que, restringidas a cada elemento de la malla, contienen un espacio de polinomios de grado dado. Las ventajas de método reside en la flexibilidad para tratar con dominios complicados y de producir espacios aproximamente de distintos grados de suavidad, y por su sólida fundamentación teórica basada en el Análisis Funcional y en la teoría de Ecuaciones Diferenciales.
Ecuaciones diferenciales fraccionarias en modelos de evolución poblacional (UNR).
Dirección: Dra. Gabriela Reyero.
Codirección: Dr. Ariel Lombardi.
Integrantes: Dra. Mélani Barrios, Est. Daiana Bravo.
Resumen: El principal objetivo de este proyecto es el de formalizar y generalizar algunos prob. de control óptimo fraccionario y sistemas de ec. diferenciales de orden fraccionario en modelos de explotación de recursos naturales y en modelos que explican la evolución en el tiempo de poblaciones de ciertas especies en competencia. En particular, se tratará de resolver prob. variacionales y de control óptimo fraccionario cuyo objetivo sea maximizar ingresos netos obtenidos de la explotación de cierto recurso y sistemas de ec. dif. fraccionarias (SEDF) de tipo depredador-presa para analizar la evolución poblacional de dos o más especies en competencia. Para ello, se realizarán análisis tanto desde el punto de vista teórico (existencia, unicidad, reg., estabilidad de sol.) como desde el punto de vista numérico (implementación de alg. de resolución, análisis de convergencia, comparación de métodos de cálculo) de ciertos prob. cuya resolución requieran de modelos con SEDF.
Estudio de modelos de orden fraccionario relativos al tratamiento de la infección por VIH y otros (UNR)
Dirección: Dr. Eduardo Santillán Marcus.
Integrantes: Dr. Alberto Ferrari, Dra. Mariela Olguín.
Resumen: Existen modelos matemáticos relativos al tratamiento de distintas infecciones, como por ejemplo la del virus de inmunodeficiencia humana (VIH), que incluyen ecuaciones diferenciales fraccionarias que describen y predicen la evolución de células sanas, infectadas y carga viral con mayor exactitud que los ya existentes con derivadas clásicas, pero que su resolución es más compleja o no ha sido totalmente desarrollada. La meta de este proyecto es realizar una actualización, profundización e investigación en temas de ecuaciones diferenciales fraccionarias relacionadas con el modelado de sistemas con memoria y su resolución aproximada o numérica.
Grupos de Lie en Geometría Pseudo y Subriemanniana (UNR)
Dirección: Dr. Silvio Reggiani.
Codirección: Dr. Francisco Vittone
Integrantes: Dra. I. Cardoso, Dr. M. Subils, Dra. G. Ovando, Lic. A. Cosgaya, Lic B. Luporini, Est. C. Rodolfo, Est. V. García.
Resumen: Los grupos y álgebras de Lie aparecen naturalmente en el estudio de diversos problemas geométricos en variedades. Estos grupos de Lie pueden verse como grupos de simetrías de un esp. (pseudo)riemanniano, como grupos que dejan invariante una cierta
estructura geom. o un operador diferencial.
En este proy. nos enfocaremos en el estudio de grupos de Lie que
aparecen:
1) como espacios (pseudo)riemannianos asociados a una métrica invariante a izq.;
2) como grupos de isometrías de variedades homogéneas pseudoriemannianas;
3) asoc. a ciertos espacios homogéneos que fibran sobre espacios simétricos de tipo compacto;
4) como el grupo de presentación de un espacio homogéneo naturalmente reductivo;
5) como el espacio ambiente donde naturalmente se estudian ciertos operadores diferenciales y sus soluciones fundamentales;
6) como el grupo de holonomía de Cartan de una variedad riemanniana.
Geometría de nilvariedades hermitianas (PICT).
Dirección: Dr. Silvio Reggiani.
Integrantes: Dr. Francisco Vittone.
Resumen: Un problema altamente no trivial es decidir cuándo una variedad de dimensión par admite una estructura compleja. Un problema adicional, en espacios que admiten estructura compleja, es el de la clasificación salvo equivalencia. En el contexto de los grupos de Lie, esto sería el problema de clasificar estructuras complejas salvo conjugación por un automorfismo de grupos de Lie. Tomando una clase relevante de nilvariedades 2-pasos, nos parece interesante entender si aparecen estructuras hermitianas para métricas con co-índice de simetría no trivial. Para resolver este problema, primero hay que describir el espacio de moduli de métricas invariantes a izquierda y luego calcular el índice de simetría para cada clase de equivalencia. Con esta información uno podría tratar de detectar si hay estructuras complejas compatibles con dichas métricas.
Estructuras geométricas en álgebras de Lie (UNR).
Dirección: Dr. Francisco Vittone.
Codirección: Dr. Silvio Reggiani.
Integrantes: Dr. Mauro Subils, Lic. Brian Luporini.
Resumen: Se pretenden clasificar los grupos de automorfismos y las clases de métricas invariantes a izquierda equivalentes en álgebras de Lie nilpotentes de dimensión 6. Se buscará además relacionar la teoría clásica de Lie con la de los sistemas triples de Jordan para el estudio de los espacios simétricos y en particular de la holonomía normal de subvariedades de formas espaciales complejas.
Geometría de espacios localmente homogéneos: geodésicas, trayectorias magnéticas e isometrías (UNR)
Dirección: Dra. Gabriela Ovando.
Codirección: Dr. Mauro Subils.
Integrantes: Lic. Pablo Montenegro.
Resumen: En este proyecto trabajamos con ciertas estructuras geométricas que pueden construirse con una data algebraica. Estudiamos ciertas trayectorias y sus flujos en variedades diferenciales munidas de una métrica riemanniana (o pseudo) localmente invariante. El foco está puesto en las trayectorias magnéticas en nilvariedades, el flujo geodésico en nil y solvariedades y su integrabilidad o no, y en los grupos de isometrías y la relación con los problemas anteriores. Las trayectorias magnéticas surgen naturalmente como una generalización de las trayectorias de partículas bajo la acción de una fuerza magnética, así como las geodésicas generalizan la trayectoria de partículas libres de fuerza.
Proyecto en gestación: Matemática para Aprendizaje Automático.
Integrantes: Dra. Isolda Cardoso, Dra. Jorgelina Walpen.
Resumen: Este espacio está siendo gestado desde principios del 2022, momento en el que nos propusimos abrirnos, desde nuestra perspectiva como matemáticas, a un área relativamente nueva y en pleno desarrollo: la del Aprendizaje Automático (Machine Learning). Proponemos tres ejes fund. de trabajo para quienes quieran sumarse. En primer lugar, consideramos imprescindible el estudio de los principios matemáticos de la Ciencia de Datos y la Inteligencia Artificial. En segundo lugar, nos interesa aplicar las herramientas del Aprendizaje Autom. para discernir, buscar patrones y conexiones con la investigación en matemática, como también aportar a la resolución de problemas matemáticos. Existen art. muy recientes al respecto, y en diversas áreas de la matemática. Finalmente, nos interesa el desarrollo matemático para la mejora de los alg. de Aprendizaje Autom. ya existentes. Este eje es quizás el más extendido y el de mayor desarrollo actualmente, aunque no necesariamente son matemáticxs quienes están haciendo los aportes. Desde nuestra formación pretendemos dar otra mirada y quizás enmarcar y profundizar algunos aspectos.
Los procesos de construcción de conocimiento acerca de la práctica docente en el Profesorado de Matemática de la Facultad de Ciencias Exactas, Ingeniería y Agrimensura de la Universidad Nacional de Rosario
Integrantes: Dra. Natalia Sgreccia, Dra. Virginia Ciccioli, Lic. Prof. Mariela Cirelli, Prof. M. Beatriz Vital, Prof. Martín Alegre, Prof. Virginia Bonservizi, Prof. Facundo Chirino, Prof. Eliana Dominguez, Prof. Valeria Donato, Prof. M. Virginia Frontini, Prof. Sabrina Grossi, Prof. Natalia Landaluce, Prof. M. Sol Mengarelli, Prof. Lucía Schaefer, Prof. Sofía Pipolo, Prof. Florencia González, Prof. Denise Rudi, Prof. Agustín Pace.
Asesora: Marta Massa
Colaboradora: Petrone Elisa
Estudiantes de grado: Lucía Primo Brochiero, Bianca Di Biaggio.
Resumen: El proyecto se enmarca en un Programa, Los procesos de construcción de conocimiento acerca de la práctica docente en carreras de grado y de posgrado de la Universidad Nacional de Rosario, dirigido por la Dra Natalia Sgreccia y codirigido por la Dra Liliana Sanjurjo. Programa, radicado en la FCEIA, al que integran además tres proyectos análogos al estudio de las prácticas en diferentes carreras de la UNR. Su vigencia es desde enero de 2022 hasta diciembre de 2025. Sostiene una concepción de conocimiento como proceso de construcción subjetivo, social, político y cultural que permite paulatinos acercamientos a la comprensión de una realidad, en este caso los procesos formativos en el campo de las prácticas profesionales docentes y el Profesorado en Matemática.
El conocimiento profesional del profesor en Matemática deviene de teorías científicas, de conocimiento experiencial construido a partir de las prácticas y está atravesado por valores y creencias. De allí la emergencia de su proceso de construcción como un desafío que ha de abordarse con rigurosidad y creatividad, y que al mismo tiempo plantea la necesidad de constituirse en objeto de investigación. Desde los enfoques hermenéutico-reflexivos y críticos la práctica es fuente de comprensión y de generación de teoría. El proyecto tiene como objetivos:
– Comprender los procesos de construcción de conocimiento acerca de la práctica docente que llevan a cabo estudiantes, graduados y docentes de la carrera de grado Profesorado en Matemática de la UNR.
– Contribuir con el avance del conocimiento científico acerca del campo de la formación en prácticas docentes en Profesorados en Matemática.