

Next: Conclusions
Up: Applications of recurrence quantified
Previous: Dynamical system, a description
If we wish to use the RQA method to a time series long enough
for reliability, we face the usual difficulties, memory capacity and
calculus complexity.
Most of the codes were developed in C under Linux operating system.
This language does not implement the Boolean data type using integer type instead,
so the required memory amount to store the recurrence matrix coming from a typical
time series of 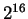 data points is 128 Gbits
data points is 128 Gbits![[*]](/usr/share/latex2html/icons/footnote.png) and,
the algorithm complexity is quadratic, which implies huge time consuming.
In order to solve these problems we propose to reduce the dimension of the
matrix
and,
the algorithm complexity is quadratic, which implies huge time consuming.
In order to solve these problems we propose to reduce the dimension of the
matrix 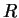 , but then the mapping may not be one to one and a whole region of
the reconstructed space would have the same points as image.
Therefore
, but then the mapping may not be one to one and a whole region of
the reconstructed space would have the same points as image.
Therefore 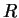 as defined in (1) is modified as:
as defined in (1) is modified as: 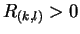 if and only if at least a pair of indexes exists
if and only if at least a pair of indexes exists
![$(i,j) \in \{(i,j) / k=[i \frac{N}{m}], \, l=[j \frac{N}{m}] \}$](img56.png) for
for 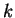 and
and 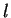 given, with
given, with
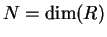 and
and 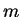 the amount data points,
such as
the amount data points,
such as
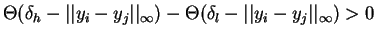 and zero otherwise.
Due to hardware limitation we use recurrence matrices 10240 x 10240 values, although
this fact was discussed before,and means a loss in the matrix resolution, the
obtained results are quite satisfactory taking into account an adjusting of
the corridor width and studying the parameters asymptotic behavior as a function
of the number of the data.
Another problem concers the RQA high sensibility with the number of
cycles during a time interval.
As is depicted in figure-1 %DET has an asymptotic value when the
number of cycles is greater than 30.
If we are dealing with a sub-harmonic cascade or in the intermittency region an
abrupt change in the number of cycles is observed, giving us false transitions
associate to the change in the cycles number.
But the number of cycles can not be so big because it produces a graphic saturation
then %DET falls on minor values. A reason is an increment in vectors amount
mapped to same
and zero otherwise.
Due to hardware limitation we use recurrence matrices 10240 x 10240 values, although
this fact was discussed before,and means a loss in the matrix resolution, the
obtained results are quite satisfactory taking into account an adjusting of
the corridor width and studying the parameters asymptotic behavior as a function
of the number of the data.
Another problem concers the RQA high sensibility with the number of
cycles during a time interval.
As is depicted in figure-1 %DET has an asymptotic value when the
number of cycles is greater than 30.
If we are dealing with a sub-harmonic cascade or in the intermittency region an
abrupt change in the number of cycles is observed, giving us false transitions
associate to the change in the cycles number.
But the number of cycles can not be so big because it produces a graphic saturation
then %DET falls on minor values. A reason is an increment in vectors amount
mapped to same 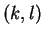 matrix component. So when this amount goes too far a
heuristic limit; determinism is lost.
Taking this into account the parametric measurements associate to the RQA
were done in such a way to use the half cycles on the plateau.
matrix component. So when this amount goes too far a
heuristic limit; determinism is lost.
Taking this into account the parametric measurements associate to the RQA
were done in such a way to use the half cycles on the plateau.
Figure 1:
%DET as a function of cycles number for PO chemical reaction.
For 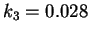 a limit cycle periodic behavior is observed. From 50 cycles the
%DET decays due to the saturation of the RP.
a limit cycle periodic behavior is observed. From 50 cycles the
%DET decays due to the saturation of the RP.
|
|
Figure 2:
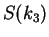 for 40 cycles, a plateau can be seen as in the chaotic
as in the periodic regions, for values in the range
for 40 cycles, a plateau can be seen as in the chaotic
as in the periodic regions, for values in the range
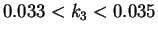 the plateau observed is an indication of the chaotic state of the system.
the plateau observed is an indication of the chaotic state of the system.
|
|
Since RP is not quite sensible to the election of the embedding dimension, 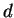 ,
we use
,
we use 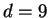 which this value allow us to eliminate the non diagonal points
in the RP plots without affecting its general structure [11].
On the other hand, no difference is observed neither
which this value allow us to eliminate the non diagonal points
in the RP plots without affecting its general structure [11].
On the other hand, no difference is observed neither 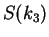 ,
or any RQA parameters within a range
,
or any RQA parameters within a range
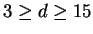 , so we use the value recommended
by Takens' theorem [4].
As it can be seen in figures-2and 3
there is no direct proportion found between
, so we use the value recommended
by Takens' theorem [4].
As it can be seen in figures-2and 3
there is no direct proportion found between
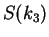 , and the maximum Lyapunov exponent
, and the maximum Lyapunov exponent 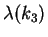 ,
by using the Aurell's algorithm et al. in TISEAN package [12]
calculated with a Thieler's window [13] with 500 time units.
Different algorithms associated with the evaluation of
,
by using the Aurell's algorithm et al. in TISEAN package [12]
calculated with a Thieler's window [13] with 500 time units.
Different algorithms associated with the evaluation of 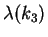 int TISEAN package were
used with unsatisfactory results due to the time consuming for getting a reliable
slope in the graphical methods.
On the other hand in figure-3 the expected plateau is not observed
in the range of values when the system is in the chaotic regime as studied by
Geest et al[7]. They have done an exhaustive numerica study of the NADH
oxidation reaction in the chaotic regime.
It is important to note as depicted in figure-2 the chaos transition
characterization since
int TISEAN package were
used with unsatisfactory results due to the time consuming for getting a reliable
slope in the graphical methods.
On the other hand in figure-3 the expected plateau is not observed
in the range of values when the system is in the chaotic regime as studied by
Geest et al[7]. They have done an exhaustive numerica study of the NADH
oxidation reaction in the chaotic regime.
It is important to note as depicted in figure-2 the chaos transition
characterization since 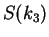 increase its value towards a plateau for the
increase its value towards a plateau for the
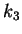 values which correspond to a sub-harmonic cascade, as well as a peak in
the neighborhood of the first bifurcation value.
values which correspond to a sub-harmonic cascade, as well as a peak in
the neighborhood of the first bifurcation value.
Figure 3:
Maximum Lyapunov exponent, 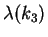 ,
found by using Aurell's et al. algorithm for 40 cycles.
The observed plateau is apparent since in that range of values the system
is aproaching to the onset of a subharmonic cascade and in the chaotic region
the algorithm does not show conclusive evidences.
,
found by using Aurell's et al. algorithm for 40 cycles.
The observed plateau is apparent since in that range of values the system
is aproaching to the onset of a subharmonic cascade and in the chaotic region
the algorithm does not show conclusive evidences.
|
|
%DET(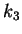 ) is associated with the existence of stable and unstable periodic orbits.
In general the probability density related with periodic orbits is uniform,
but for a dense family of unstable orbits, it has an exponential distribution since
it is more probable to find our systems orbits with shorter period.
For us, %DET
) is associated with the existence of stable and unstable periodic orbits.
In general the probability density related with periodic orbits is uniform,
but for a dense family of unstable orbits, it has an exponential distribution since
it is more probable to find our systems orbits with shorter period.
For us, %DET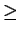 99% always, and the behavior
in the chaotic region is the same as
99% always, and the behavior
in the chaotic region is the same as 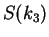 ,
that means the increasing number of periodic orbits
due to the sub-harmonic cascade from
,
that means the increasing number of periodic orbits
due to the sub-harmonic cascade from 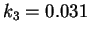 up to reach a maximum in the
chaotic region densely populated by unstable orbits. For
up to reach a maximum in the
chaotic region densely populated by unstable orbits. For 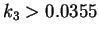 the number of orbits is considerably reduced after an intermittent behavior.
This is intrinsic to our dynamical system since it is not observed in the
Lorentz system, used as a toy model [11]in this trail.
On the other hand, by analyzing %REC(
the number of orbits is considerably reduced after an intermittent behavior.
This is intrinsic to our dynamical system since it is not observed in the
Lorentz system, used as a toy model [11]in this trail.
On the other hand, by analyzing %REC(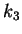 ) we may appreciate the scarce
population of recurrent points in the RP. %REC holds a constant value and is
reduced at the beginning of the cascade with a minimum in the chaotic
region. This behavior is different of that observed with %DET and
) we may appreciate the scarce
population of recurrent points in the RP. %REC holds a constant value and is
reduced at the beginning of the cascade with a minimum in the chaotic
region. This behavior is different of that observed with %DET and 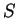 augmenting
the value up to get a lower plateau. We assume this can be due to the changes
in the shape of the attractor, since the same results is obtained for the Lorentz
system [11].
By a simple inspection in the RP the increasing number of periodic orbits is clear,
because more parallel lines to the diagonal appear, but the changes in the attractor
shape are less impressive and can only be appreciate as skewed curves when the
embedding dimension is near
augmenting
the value up to get a lower plateau. We assume this can be due to the changes
in the shape of the attractor, since the same results is obtained for the Lorentz
system [11].
By a simple inspection in the RP the increasing number of periodic orbits is clear,
because more parallel lines to the diagonal appear, but the changes in the attractor
shape are less impressive and can only be appreciate as skewed curves when the
embedding dimension is near 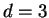 .
.


Next: Conclusions
Up: Applications of recurrence quantified
Previous: Dynamical system, a description
Horacio Castellini
2004-10-27
![\includegraphics[width=7cm, height=5cm]{f1.ps}](img62.png)
![\includegraphics[width=7cm, height=5cm]{f1.ps}](img62.png)
![\includegraphics[width=7cm, height=5cm]{f2.ps}](img63.png)
![\includegraphics[width=7cm, height=5cm]{f3.ps}](img67.png)