

Next: Acople SA
Up: MODELIZADO DEL GENERADOR CENTRAL
Previous: Modelo de GCP usado
Independientemente del tipo de elección de acoplamientos,
SA ó SB,
aparece un comportamiento en función del retardo de tiempo,
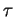
![[*]](/usr/share/latex2html/icons/footnote.png) , bastante robusto
ante variaciones del parámetro
, bastante robusto
ante variaciones del parámetro 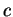 en la ec. 6. A medida
que se incrementa el retardo (partiendo de
en la ec. 6. A medida
que se incrementa el retardo (partiendo de 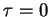 ) aparece
un pasaje de caos
) aparece
un pasaje de caos  oscilaciones armónicas
oscilaciones armónicas  punto
estacionario estable
punto
estacionario estable
 bifurcación de Hopf primaria
bifurcación de Hopf primaria  bifurcación de Hopf
secundaria
bifurcación de Hopf
secundaria  caos. El comportamiento caótico fue ratificado estudiando los máximos
exponentes de Lyapunov por medio del paquete TISEAN[21].
caos. El comportamiento caótico fue ratificado estudiando los máximos
exponentes de Lyapunov por medio del paquete TISEAN[21].
Figura 1:
Máximo exponente de Lyapunov, 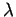 obtenido de una serie
temporal de valores de salidas sobre una celda del anillo. Se utilizó
el algoritmo de Aurell et al. provisto por el paquete de cálculo
TISEAN[21].
obtenido de una serie
temporal de valores de salidas sobre una celda del anillo. Se utilizó
el algoritmo de Aurell et al. provisto por el paquete de cálculo
TISEAN[21].
|
|
En la figura-1 se puede observar el comportamiento del máximo
exponente de Lyapunov, 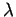 en función del retardo. La meseta
corresponde a valores de
en función del retardo. La meseta
corresponde a valores de 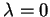 , lo cuál indica una oscilación
armónica, en cambio para el resto de los valores de retardo toma un valor
, lo cuál indica una oscilación
armónica, en cambio para el resto de los valores de retardo toma un valor
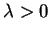 . Esto corresponde a la presencia de un comportamiento caótico
del sistema.
Si bien esto parece poco relevante
a la hora de evaluar las simetrías, no lo es respecto al tiempo que
dura cada patrón, pues una inestabilidad en los tiempos puede
ser nociva para un andar regular.
Y es menester conocer para que valores de retardo el intervalo de
tiempos que dura cada patrón se torna inestable. En general, tanto para
. Esto corresponde a la presencia de un comportamiento caótico
del sistema.
Si bien esto parece poco relevante
a la hora de evaluar las simetrías, no lo es respecto al tiempo que
dura cada patrón, pues una inestabilidad en los tiempos puede
ser nociva para un andar regular.
Y es menester conocer para que valores de retardo el intervalo de
tiempos que dura cada patrón se torna inestable. En general, tanto para
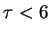 como para
como para 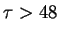 los intervalos de tiempos tienen varianza
elevada, por lo que se limitará el intervalo de retardo al intervalo
los intervalos de tiempos tienen varianza
elevada, por lo que se limitará el intervalo de retardo al intervalo
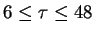 .
.
Subsecciones


Next: Acople SA
Up: MODELIZADO DEL GENERADOR CENTRAL
Previous: Modelo de GCP usado
Horacio Castellini
2004-10-27