
Una señal limitada en banda x(t), es decir, que no posee ninguna componente de frecuencia superior a wm, puede, en teoría, ser perfectamente reconstruida a partir de una señal xs(t) resultante de un muestreo de la original (si se verifica que la frecuencia de muestreo ws es mayor que la máxima de la señal wm). Sin embargo, el proceso de muestreo y reconstrucción es complicado y existen dificultades inherentes a la representación de señales de tiempo continuo en una computadora, que se enuncian a continuación.
Para permitir al usuario modificar los valores de las señales con el mouse, SampleMania representa internamente a las señales de tiempo continuo como señales de tiempo discreto donde cada pixel se corresponde con una muestra. De esta forma, una señal suave de tiempo continuo, como ser una onda senoidal, se comporta como una señal digital con muy pequeños saltos cuando se la observa en intervalos de tiempo muy reducidos. Esto se muestra en la siguiente curva:

El resultado de esta aproximación es un agregado de señal de alta frecuencia que no existiría en la representación de la onda de tiempo continuo. A continuación se observa la diferencia entre el espectro de magnitud esperado para una onda de tipo senoidal (gráfica a la derecha) y el resultante a causa de la discretización inherente a la representación a base de pixels.
Otra aproximación es la efectuada sobre las señales generadas por los botones Sine y Sinc, ya que estos generan versiones limitadas en el tiempo de las ondas seno y sinc. Es decir, si bien las funciones deberían ser de duración infinita, SampleMania las recorta haciéndolas cero en el exterior de la ventana representada.
Como resultado de esto, se tiene, por aplicación de una propiedad de la transformada de Fourier, que el espectro de la señal representada será la convolución entre la transformada de la onda requerida y la de un pulso de duración igual a la ventana representada. Esto es así porque se puede pensar a la onda representada como el resultado de una multiplicación temporal entre la señal deseada y el pulso de amplitud unitaria y duración igual a la ventana mostrada. Recordando que un producto en las señales temporales implica una convolución en el dominio frecuencial y viceversa, se llega a que el espectro de la señal representada es el resultado de una convolución frecuencial.
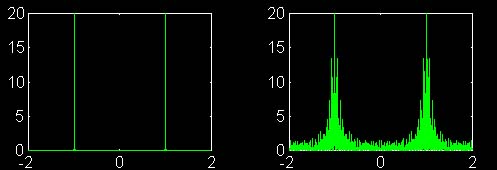
Siendo la transformada de un pulso rectangular una función sinc, y por dualidad, la de una función sinc un pulso rectangular, se tendrá que para un pulso de duración infinita (función constante), su transformada se aproximará a un impulso, mientras que por otro lado a medida que se hace más angosto el pulso, tendiendo a un impulso, su transformada tiende a una constante. Esto se visualiza en las siguientes gráficas:

Con lo que el espectro correspondiente a la señal sinc generada por SampleMania será la convolución del verdadero espectro (un pulso rectangular) y una sinc correspondiente a la transformada del pulso que restringe el tiempo a la ventana mostrada. Como resultado, se tiene que el espectro de esta señal nunca se anula, por ser la sinc (transformada del pulso rectangular) una función de duración infinita, esto trae aparejado un efecto de aliasing al muestrear la señal, por no ser ésta una del tipo limitada en banda. A continuación se muestra el espectro de dos ondas sinc, la primera limitada a una ventana de tiempo de [-1000;1000] y la otra en una de [-300;300], se puede apreciar el mayor contenido de alta frecuencia de la segunda onda respecto de la primera, pero notando que ninguna es realmente limitada en banda por no ser ondas de duración infinita en el tiempo.

Puede ocurrir que la región filtrada del espectro de magnitud correspondiente a la señal muestreada difiera del correspondiente a la señal reconstruida. Existen varias razones para esto, primero, la reconstrucción no es llevada a cabo en el dominio frecuencial con un filtro pasa bajos, sino en el dominio temporal a través de una convolución con una sinc (se hace para evitar los cálculos implicados en la antitransformación). Si bien estos dos procesos son equivalentes en teoría, la imprecisión en el cálculo de la sinc como el hecho de utilizar una sinc restringida a la ventana de tiempo mostrada pueden provocar una reconstrucción con imperfecciones.
Otra razón recae en el hecho de utilizar un algoritmo diferente para el cálculo del espectro de la señal muestreada respecto del utilizado para las señales original y reconstruida. La razón de esto es que, al ser la frecuencia de muestreo especificada como un determinado número de radianes por segundo (o bien en hz), con lo cual la cantidad de pixels en cada período de muestreo puede ser irracional. Como resultado de la utilización de un proceso de visualización estándar, para el espectro de magnitud periódico correspondiente al tren de impulsos, se tendría que para cada período sucesivo la posición del pixel correspondiente sería distinta. Esto haría que el gráfico no pareciera periódico. En el ejemplo siguiente se muestra una función senoidal de período 2p , sobre la misma se muestran los pixels espaciados en una unidad cada uno sobre el eje x. Al eliminar la curva de tiempo continuo (gráfica de la derecha), los pixels resultantes no parecen representar una función periódica.

Para compensar esto es que SampleMania utiliza un método particular para calcular las posiciones enteras de los pixels cuando se muestra el espectro de magnitud de la señal muestreada. Este algoritmo puede provocar pequeñas discrepancias entre el espectro de la señal muestreada y el de la señal reconstruida.
Regresar a la página de muestreo y reconstrucción de señales
en tiempo continuo (rad/seg)
Regresar a la página de muestreo y reconstrucción de señales
en tiempo continuo (Hertz)