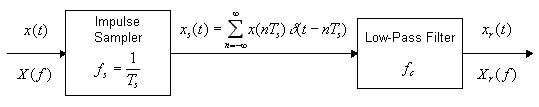
Una señal de tiempo continuo, x(t) se muestrea a una frecuencia de f_s hz, obteniéndose una señal muestreada x_s(t). Modelamos x_s(t) como un tren de impulsos, donde el área del n-ésimo impulso esta dada por x(nT_s). Un filtro pasa-bajos ideal con frecuencia de corte f_c hz, es utilizado para obtener la señal reconstruida x_r(t).

Supongamos que la componente de frecuencia más alta en x(t) es f_m. Entonces, por el teorema del muestreo, se asegura que para f_s > 2.f_m no habrá pérdida de información en el muestreo. En este caso, eligiendo una f_c en el rango f_m > f_c > f_s - f_m se verificará x_r(t)= x(t). Este resultado puede ser entendido al observar las transformaciones de Fourier de X(f), X_s(f) y X_r(f). Si no se verificara el teorema del muestreo (f_s < 2.f_m) y/o f_c se eligiera fuera del rango indicado, se tendrá como resultado que x_r(t) diferirá de x(t) producto de la aparición de "aliasing".

Para observar ejemplos de muestreo y reconstrucción, seleccione una señal preestablecida o bien mediante el uso del mouse dibuje una forma de onda para x(t), en la siguiente ventana. Luego de un momento, se trazará en la ventana de la izquierda el espectro de magnitud |X(f)| correspondiente a la señal seleccionada y/o creada. Luego, las cuatro ventanas inferiores se agrupan de a pares, permitiendo comparar efectos de muestreo y reconstrucción para dos frecuencias de muestreo distintas así como también para dos frecuencias de corte del filtro pasa-bajos ideal distintas. Pudiéndose observar los diferentes espectros de magnitud resultantes, y las correspondientes funciones temporales.

 Notas sobre la implementación computacional

Pasar a página basada en Rad/Segs

Volver a página de Demos