Ejemplo 5

H = 0 Hallar los extremos relativos de :                                                             f (x,y) = x2 y2 Analizando el sistema                                   f x (x, y) =  0                                  f y (x, y) = 0 se obtiene que son puntos críticos todos aquellos cuyas coordenadas son  del tipo (0, y)  para todo y ( recta x = 0 ) y además  los puntos cuyas coordenadas son del tipo (x,0) para toda x ( recta y = 0 ). Para todos esos puntos resulta H (x,y) = 0, por tanto el criterio de las derivadas parciales  segundas no decide. Sin embargo como f (x, y) > 0 para todo punto del plano salvo en las rectas x = 0, ó y = 0 donde  f (x, y) = 0, podemos concluir que todos los puntos de estas dos rectas (puntos críticos de f ), son mínimos absolutos de la función.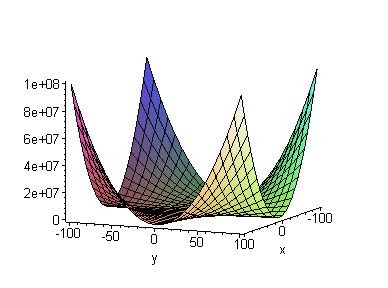