Los posibles puntos críticos se obtienen resolviendo el siguiente sistema:

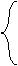	fx = 2 x = 0
	fy = -2 y = 0

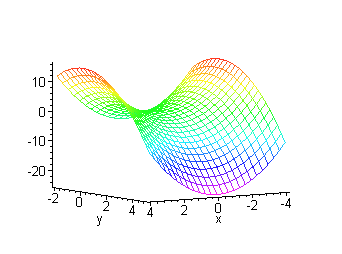
El único punto crítico es el ( 0, 0 ), pero en ese punto no se produce máximo ni mínimo.

Este punto se llama punto silla o de ensilladura

                  Definición :

Sea (a,b) un punto crítico de f.

El punto (a,b,f(a,b))  es punto silla de f  sí y sólo sí en todo disco abierto

 centrado en (a,b) existen puntos (x₁,y₁) y (x₂,y₂) donde se verifica que 

f (x₁,y₁) > f (a,b)     y      f (x₂,y₂) < f (a,b)

En nuestro caso el disco está centrado en (0,0).Existen puntos (0.1, 0.2) y (0.2, 0.1),  por ejemplo, tales que : f(0.1,0.2) < f(0,0)  y  f(0.2,0.1) > f(0,0)                                                                                                       

En el mapa de contorno se observa que el punto donde se anulan las derivadas parciales primeras ya no es centro de las curvas como en el ejemplo anterior