 |
EXTREMOS DE
FUNCIONES DE DOS VARIABLES |
 |
 |




|
|
|
Ejemplo 1
fx=0 y fy=0
|
| Determinar
los extremos relativos de la función: |
|
f
(x,y)
= 2x2 + y2 + 8x - 6y + 20
|
 |
|
Hallamos
los puntos críticos de f:
fx
(x,y)
= 4x + 8 = 0
fx
(x,y)
= 2y - 6 = 0
|
|
Resolvemos
ese sistema de ecuaciones y obtenemos que el único punto crítico
es (-2,3).
Completando
cuadrados
f
(x,y)
= 2(x + 2)2 + (y - 3)2 + 3 > 3,
para todo
(x,y) ≠ (-2,3), por lo tanto, hay un mínimo
de f en (-2,3).
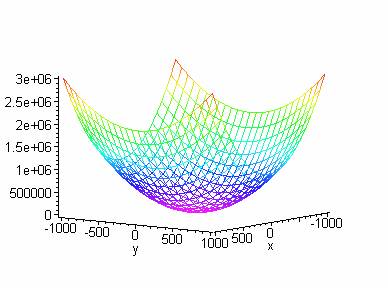
El
valor del mínimo relativo es f(-2,3) = 3, que también es un
mínimo absoluto. Como se ve en la
figura.
|
| |
Utilizando Maple, las sentencias para
graficar f serían:
> with(plots):
> f:=(x,y)-> 2 * x ^ 2 + y ^ 2 + 8 * x - 6 * y + 20;
> plot3d(f(x,y),x=-100..100,y=-100..100);
|
|
|
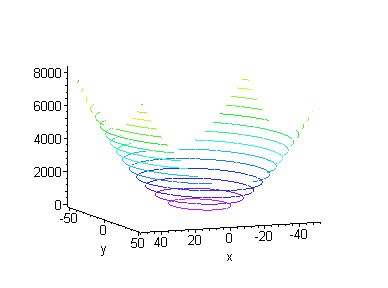 |
Curvas
de contorno
Son las curvas que se obtienen de la intersección
de una superficie de ecuación z = f (x, y) y el
plano paralelo al plano x y cuya ecuación
es z = k
 |
z = f (x, y) |
| z = k |
|
|
|
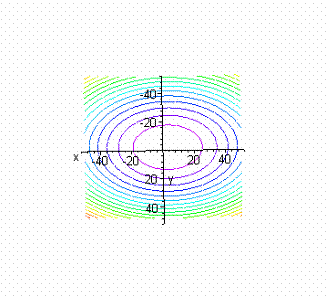
Curvas de nivel
Cada una de las curvas de contorno proyectada
sobre el plano x y,con indicación de la cota.
Al conjunto de las curvas de nivel
se lo suele llamar mapa de contorno.
Observación
El extremo relativo es el centro de las
curvas cerradas
|
| |
Utilizando Maple, la sentencia para
obtener el mapa de contorno es:
>contourplot(f(x,y),x=-100..100,y=-100..100);
|
|
|
|
Puede que fx(a,b)=fy(a,b)=0 y sin embargo
f(a,b) no es extremo, por ejemplo.. |
|
|
|
| |
Profs.
-Graciela Paván - Ana Sadagorsky |
|
