|
Extremos absolutos en un dominio cerrado Encontrar
los extremos absolutos de la función f (x, y) = sen (x y) en la
región cerrada dada por:
0 ≤ x ≤ π y 0 ≤ y ≤ 1.
a) Puntos interiores: 0 < x < π, 0 < y < 1
| fx (x, y) = y cos (x y) = 0
fy (x, y) = x cos (x y)
= 0 |
|
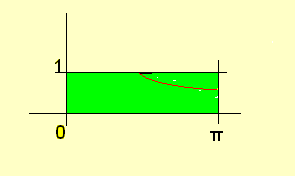 |
Resolviendo el sistema, y teniendo en cuenta que la región considerada es la de color verde, se deduce que cada punto de la hipérbola de ecuación:
x . y = π / 2
es un punto crítico.
En cada uno de estos puntos, f (x, y) = sen (x y) = sen( π / 2) = 1
b) Puntos frontera
Consideremos un lado del rectángulo a la vez
i) Para y = 1, 0 ≤ x ≤ π
si x = 0 entonces f ( 0, 1) = sen 0 = 0
si x = π entonces f ( π , 1) = sen π = 0
Estudiemos, estudiemos ahora, en los puntos interiores a la recta y = 1, con 0 < x < π
f (x, y) = f ( x, 1) = sen x = g (x)
g' (x) = cos x = 0 en x = π / 2
f ( x, 1) = f ( π / 2, 1) = 1
ii) Para x = π 0 ≤ y ≤ 1
si y = 0 f (π, 0) = sen 0 = 0
si y = 1 f ( π, 1) = sen π = 0
Estudiemos en los puntos interiores a la recta x = π con 0 < y < 1
f ( π, y) = sen ( π y) = h (y)
h' ( y) = π cos ( π y ) = 0 cuando π. y = π/2, o sea cuando y = 1/2
iii) En el intervalo y = 0, 0 ≤ x ≤ π
si x = 0 , f (0, 0) = sen( 0. 0) = 0
si x = π , f (π ,0) = 0
Estudiemos en los puntos interiores a la recta y = 0 con 0 < x < π
f (x, 0) = sen (x.0) = sen 0 = 0
iv) En el intervalo x = 0, 0 ≤ y ≤ 1
si y = 0 , f (0, 0) = 0
si y = 1, f ( 0, 1) = 0
Estudiemos en los puntos interiores a la recta x = 0 con 0 < y < 1
f ( 0,y) = sen ( 0 y) = 0
Conclusión:
El mínimo absoluto se obtiene en todos los puntos del eje x, eje y, así como en el punto de coordenadas ( π, 1 )
El máximo absoluto se obtiene en cada uno de los puntos de la hipérbola de ecuación : x . y = π / 2
|