Resolución práctica 0
A continuación presentamos soluciones a los ejercicios de la Práctica 0.
Como siempre, en el proceso de resolución de un problema, primero debemos dedicar un tiempo al análisis del mismo para asegurarnos de entender correctamente qué se pide. Luego, pasamos a la resolución propiamente dicha.
Recomendamos usar este documento como un elemento de ayuda y referencia. Es importante que no lean la solución sin antes haber leído y entendido el problema y sin haber dedicado un tiempo a pensar cómo resolverlo.
Por otro lado, no hay una única forma correcta de escribir una solución.
1 Definiendo Funciones
Veremos resoluciones a algunos de los ejercicios de la sección 6.2.
1.1 Ejercicio 3
Es muy importante desarrollar cierta disciplina a la hora de escribir código que resuelva un determinado problema o cumpla una determinada función. Una MALA práctica de programación es tratar de escribir código sin antes haber dedicado tiempo a pensar el problema en sí, independientemente del medio por el cual materialicemos su solución (en nuestro caso, código racket). Lo recomendable es comenzar pensando el problema teniendo a mano lápiz y papel.
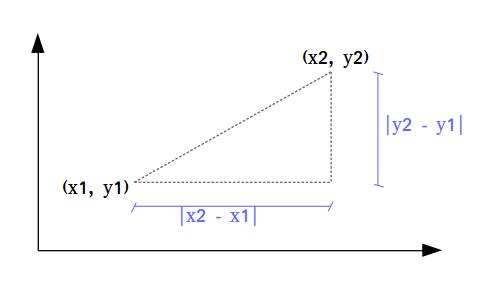
En este ejercicio, debemos calcular la distancia entre los puntos (x1 ,y1) y (x2 ,y2). Al trabajar con elementos de geometría, suele ser útil graficarlos.
Observamos que la distancia a calcular es la longitud de la hipotenusa del siguiente triángulo rectángulo que determinan esos dos puntos:
Es decir que debemos calcular la longitud de la hipotenusa de un triángulo rectángulo con catetos cuyas longitudes son el valor absoluto de la diferencia entre x2 y x1 y el valor absoluto de la diferencia entre y2 e y1. Para resolver esto, usamos el teorema de Pitágoras. Con lo cual, ahora podemos escribir:
(define (cuadrado num) (* num num))
(define (distancia-entre-puntos x1 y1 x2 y2) (sqrt (+ (cuadrado (- x2 x1)) (cuadrado (- y2 y1)))))
Nótese que no fue necesario calcular el valor absoluto de un número. ¿Por qué?.
Por otro lado, también podríamos haber dado la siguiente solución:
(define (distancia-entre-puntos2 x1 y1 x2 y2) (sqrt (+ (* (- x2 x1) (- x2 x1)) (* (- y2 y1) (- y2 y1)))))
Sin embargo, la primera opción es mejor, por varios motivos:
Claridad.
Reuso. La operación de elevar un número al cuadrado es bastante usual. Con lo cual, si definimos una función que la implemente, podemos reutilizarla después, en otra situación. De hecho, racket tiene una función para ello, llamada sqr, con lo cual podríamos haber escrito directamente:
(define (distancia-entre-puntos x1 y1 x2 y2) (sqrt (+ (sqr (- x2 x1)) (sqr (- y2 y1)))))
Menos propenso a errores. En general, es preferible aislar funcionalidades diferentes en funciones diferentes. Tener más funciones, pero más "chicas" facilita también los procesos de buscar y solucionar posibles errores, que en computación llamamos testing y debug, respectivamente.
1.2 Ejercicio 5
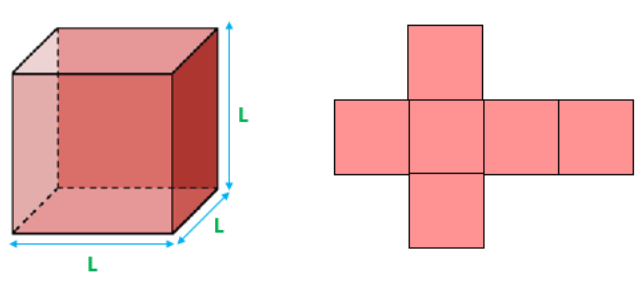
Un cubo es un poliedro regular formado por 6 caras cuadradas iguales, tal como se ve en las siguientes imágenes:
Sabemos que el área de un cuadrado es igual a la longitud de cualquiera de sus aristas elevada al cuadrado. En Racket podemos escribir una función que calcula el área de un cuadrado a partir de la longitud de sus aristas de la siguiente forma:
(define (area-cuadrado arista) (* arista arista))
Luego, conociendo el área de uno de los cuadrados que conforman la superficie del cubo, podemos escribir una función que calcula su área multiplicando ese valor por 6:
(define (area-cubo arista) (* (area-cuadrado arista) 6))
1.3 Ejercicio 8
Debemos pensar cuándo tres números pueden representar las longitudes de los lados de un triángulo. La desigualdad triangular nos dice que en todo triángulo la suma de las longitudes de dos lados cualesquiera es siempre mayor a la longitud del lado restante.
Por lo tanto, una posible solución es comprobar que para cada lado del triángulo se cumple la propiedad. Es decir:
a < (b + c), b < (a + c), c < (a + b)
Esto lo podemos escribir en Racket a través de la siguiente definición:
(define (posible? a b c) (and (< a (+ b c)) (< b (+ a c)) (< c (+ a b))))
Nótese que esta nueva definición hace una única comparación en lugar de tres. ¿Por qué es también correcta?
Otra forma de expresar la propiedad de la desigualdad triangular es la siguiente:
(define (posible? a b c) (< (max a b c) (- (+ a b c) (max a b c))))
1.4 Ejercicio 11
Para definir la función pedida, se puede tomar el primer caracter del string dado y comparar a ver si es igual al caracter "A".
El problema es que vamos a recibir un error si intentamos compararlos con el operador = que venimos usando hasta ahora. Esto se debe a que dicho operador se usa para revisar igualdad entre valores numéricos. Para poder comparar strings, necesitaremos usar un operador propio para ese tipo de dato: string=?.
De esta forma, una posible solución es:
¿Qué crees que ocurrirá si llamamos a la función con un string vacío como argumento?
(define (comienzaA? string) (string=? "A" (string-ith string 0)))
Con nuestra definición actual, recibiremos un error al intentar ver si un string vacío comienza con "A". Eso se debe a que estaríamos tratando de obtener el primer elemento de un string vacío, el cual no existe.
Más adelante veremos cómo lidiar con casos específicos inusuales en nuestros programas, ya que es deseable que nuestra función pueda devolver un resultado con cualquier valor de argumento y no falle ante un caso no previsto.
1.5 Ejercicio 12
Nuestro objetivo es insertar el caracter - en la posición n de la string s.
Siempre es mejor comenzar un problema viendo un ejemplo (en especial usando hoja y papel). Si tomo "Hola mundo" y quiero insertarle el caracter en la posición 3, quedaría así:
"Hol-a mundo"
¿Cómo fue el proceso de generar la respuesta en mi cabeza? Primero cuento 3 posiciones en el string, luego tomo lo que me quedó antes, le inserto un - y sigo escribiendo mi string.
Entonces hay 3 procesos. Primero quedarme con la primer parte de la string, luego el resto y en el medio "insertar un -". Para resolver esto tengo 3 operaciones (conocidas) para utilizar en strings: substring, string-length y string-append
Nótese que mi n debe ser menor a la longitud de la string. ¿Por qué? ¿Qué pasaría si lo excediera?
"Partir" una string en dos partes se puede realizar con un substring. Podriamos definir funciones auxiliares para que quede más claro:
(define (principioS s n) (substring s 0 n))
(define (finalS s n) (substring s n (string-length s)))
Donde principioS me da la string hasta la posición n, y finalS me da la string desde n hasta el final de la string (o sea hasta su longitud).
Luego, solo nos quedaría insertar el - en el medio, y esto lo podemos hacer con string-append:
(define (poner- s n) (string-append (principioS s n) "-" (finalS s n)))