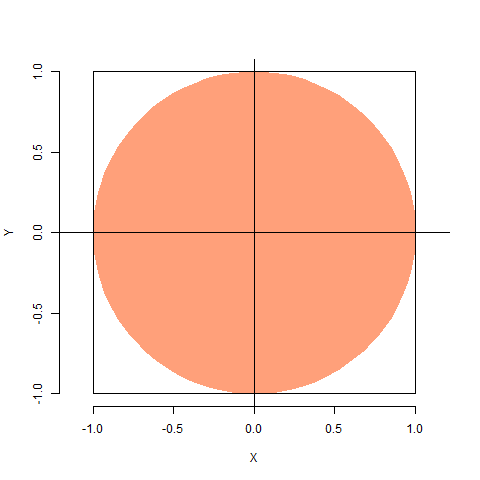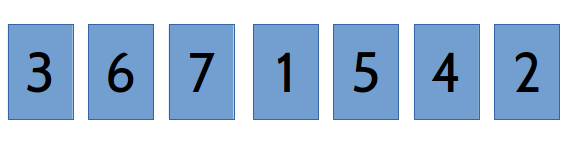Práctica 7 - Ejercicios Integradores
Programación I
1 Experimentos aleatorios
Ejercicio 1. Según la profesora de probabilidad y estadística, al tirar muchas veces un dado -si este no está cargado- la frecuencia con la que ocurre cada número tiende a ser la misma. Es decir, si tiramos un dado de seis caras doce millones de veces y anotamos los resultados, es de esperar que cada cara del dado aparezca aproximadamente dos millones de veces.
(define CARAS 6)
Diseñe una función simular-dado, que reciba un número natural n y devuelva una lista con n números aleatorios entre 1 y CARAS.
(define MAX 60000) (define EXPERIMENTO (simular-dado MAX)) (define VALORES (intervalo CARAS))
Diseñe la función frecuencia, que dado un número natural n y una lista de naturales, devuelve la cantidad de veces que n aparece en la lista. Es decir, su frecuencia absoluta.
(define (frecuencia-relativa n l) (/ (frecuencia n l) (length l)))
(define (frec-rel-exp n) (frecuencia-relativa n EXPERIMENTO))
Usando map, podemos calcular las frecuencias relativas de cada valor en el experimento:
(define FRECUENCIAS-RELATIVAS (map frec-rel-exp VALORES))
¿Qué valor de frecuencia aproximado debería repetirse en la lista FRECUENCIAS-RELATIVAS? Antes de proceder a evaluar en DrRacket, piense. Luego, evalúe.
Experimente con diferentes valores para MAX. Para estar más cerca del valor esperado, ¿MAX debe ser más grande o más chico?
¿Qué pasa si usamos 2 como valor para CARAS? ¿Qué frecuencias relativas deberíamos esperar? ¿Qué experimento estaríamos simulando?
Repita las preguntas del ítem anterior, pero con CARAS = 37.
Considere ahora que el experimento es tirar dos dados de seis caras. En este caso, la frecuencia esperada para cada resultado posible no es la misma. Diseñe un programa que calcule las frecuencias relativas de todos los posibles valores del experimento, tomando como base el programa de más arriba. Los cambios no deberían ser muchos.
2 El método de Montecarlo
El Método de Montecarlo es un método numérico estadístico usado para aproximar expresiones matemáticas. En general, este método se usa cuando obtener una solución exacta es imposible o muy costoso computacionalmente.
En esta práctica, lo utilizaremos para aproximar valores y calcular áreas o volúmenes, aunque tiene muchas otras aplicaciones a la física, la matemática y la economía, destacándose sus aplicaciones en la teoría de juegos.
2.1 Aproximando áreas
Consideremos la siguiente figura:
Imaginemos que queremos estimar el área del círculo sombreado. El método Montecarlo nos sugiere lo siguiente:
Coloquemos la figura cuya área queremos estimar dentro de otra cuya área sea conocida. En este caso, tomamos el cuadrado de lado 2 (y área 4).
Generemos de forma aleatoria un punto dentro del cuadrado, y anotemos si este punto cae dentro de la figura. Repitamos este experimento un gran número de veces.
Como la probabilidad que uno de los puntos generados caiga dentro de la figura es proporcional a su área, podemos realizar la siguiente estimación, calculando la proporción de puntos que cayeron dentro:
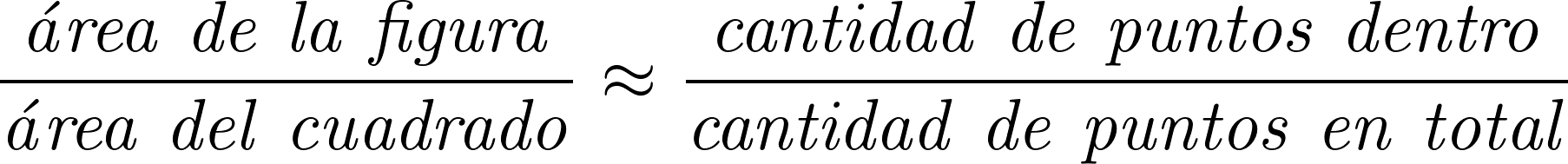
Despejando:
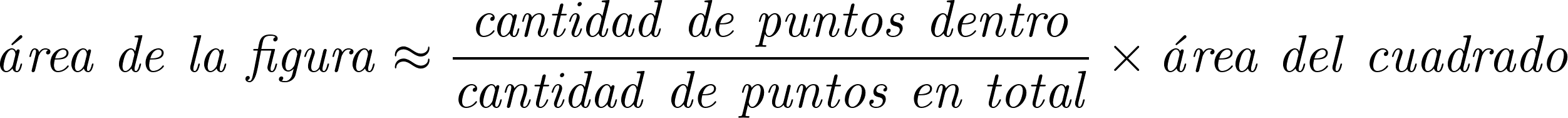
El archivo montecarlo-pi.rkt tiene un programa que implementa estas ideas para calcular el área del círculo de la figura.
2.2 Más estimaciones con círculos
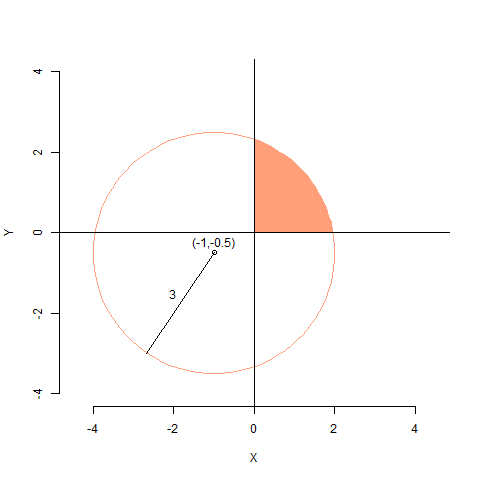
Ejercicio 2. Modifique el programa anterior para calcular el área sombreada en la siguiente figura:
El círculo está centrado en el punto (-1 ,-0.5), y tiene radio 3. Observe que en este caso no es tan sencillo predecir cuál es el resultado. Los cambios al programa original deberían ser muy pequeños. Piense primero en qué cuadrado inscribirá el área sombreada. No hace falta que contenga al círculo, sólo es necesario que contenga la superficie cuya área queremos aproximar.
3 Números primos
Decimos que un número natural n mayor o igual que 2 es primo si sus únicos divisores positivos son 1 y n. Los números que no son primos se llaman compuestos. El Teorema fundamental de la aritmética nos dice que todo número entero positivo o bien es primo, o bien puede expresarse como el producto de números primos de forma única. Hace más de 2000 años Euclides demostró que existen infinitos números primos.
Determinar si un número arbitrario n es primo es un problema computacionalmente difícil para grandes valores de n. En la dificultad de este problema basan su seguridad muchos algoritmos de encriptación. Por ejemplo, el popular sistema de criptografía de clave pública-privada RSA.
3.1 La Criba de Eratóstenes
En el siglo III antes de Cristo, el filósofo Eratóstenes describió un método para encontrar todos los números primos hasta un número predeterminado n.
Se marca el primer elemento -llamémosle k- como número primo.
Se borran todos los múltiplos de k de la lista (salvo k).
Una vez finalizado este procedimiento, tenemos la garantía que los números que quedaron marcados son todos los números primos entre 2 y n.
Para utilizar las funciones que operan sobre archivos debe cargar el paquete de enseñanza batch-io.
3.2 Verificando primalidad
La criba de eratóstenes nos permite generar una lista con todos los primos hasta un cierto número. Sin embargo, muchas veces sólo necesitamos verificar si un número m es primo o compuesto. Si bien podríamos generar la criba de eratóstenes hasta m y luego ver si m quedó sin tachar (y por lo tanto es primo), esto puede resultar computacionalmente costoso, por lo que debemos buscar otra alternativa.
Como vimos en clase, y es conocido desde hace siglos,
si m no tiene divisores primos menores o iguales que
, entonces m es primo.
Imagine que alguien nos provee un archivo cuyo contenido son los números primos hasta 10000 (un número por línea). Leyendo dicho archivo, deberíamos ser capaces de definir una lista de números cuyos elementos sean estos valores. Si llamamos a dicha lista LISTA-DE-PRIMOS, tendriamos algo como
(define MAX 10000) (define LISTA-DE-PRIMOS ....)
Observe que un número 
es primo si y sólo si no
tiene algún divisor en LISTA-DE-PRIMOS. Es decir, podemos
determinar la primalidad de números hasta 100.000.000 construyendo la criba sólo hasta 10.000.
Las funciones read-file y/o read-csv-file pueden ser de utilidad.
Haciendo uso del archivo "primos.txt" creado en el ejercicio anterior, defina la constante LISTA-DE-PRIMOS como la lista de los números primos entre 2 y 10000.
Diseñe un predicado es-primo? que dado un nátural m menor o igual que
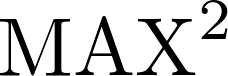determine si este es primo o compuesto.Generalice el diseño anterior mediante una función todos-primos?, que dada una lista de números menores o iguales a
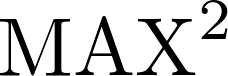, determine si todos ellos son primos. Para los casos de test, tal vez le interese saber que
86077909, 96928157, 49987169 y 54257153 son primos (debería ser más sencillo encontrar ejemplos de números que no lo son).
4 Criptografía
La Criptografía se encarga del estudio de técnicas para intercambiar información de forma segura frente a la presencia de terceras partes (llamadas normalmente adversarios). Es un área importante y con muchas aplicaciones dentro de las ciencias de la computación, en particular en lo referido a seguridad informática.
4.1 El cifrado del César
El Cifrado del César es un mecanismo de criptografía simétrica muy simple, en la cual el emisor y el receptor utilizan una clave previamente conocida para codificar y decodificar mensajes.
Una letra en el texto original es reemplazada por otra letra que se encuentra un número fijo de posiciones más adelante en el alfabeto. Por ejemplo, con un desplazamiento de 3, la A sería sustituida por la D (situada 3 lugares a la derecha de la A), la B sería reemplazada por la E, etc. Este método debe su nombre a Julio César, que lo usaba para comunicarse con sus generales. El valor de desplazamiento es la clave del método.
Ejercicio 5. En el archivo cesar-subir.rkt se encuentra una implementación incompleta del método del César. Se pide completar las definiciones faltantes. Puede además incorporar todas las funciones auxiliares que crea conveniente.
(define ALFABETO "ABCDEFGHIJKLMNÑOPQRSTUVWXYZ 0123456789") (define CLAVE 3) (define CODIGO-DEL-CESAR (cifrado CLAVE ALFABETO))
y evaluamos las siguientes expresiones
(encriptar-mensaje "HOLA" ALFABETO CLAVE) (encriptar-mensaje "ATACAR A LAS 18" ALFABETO CLAVE) (encriptar-mensaje "LA OPERACION ES REVERSIBLE" ALFABETO CLAVE) (desencriptar-mensaje (encriptar-mensaje "LA OPERACION ES REVERSIBLE" ALFABETO CLAVE) ALFABETO CLAVE)
obtenemos
"KRÑD" "DWDFDU2D2ÑDV24B" "ÑD2RSHUDFLRP2HV2UHYHUVLEÑH" "LA OPERACION ES REVERSIBLE"
5 Jugando al solitario
Entre clase y clase, Francisco suele jugar al solitario "Nada en su lugar". Este juego se juega con un mazo de N cartas, numeradas del 1 al N. Por ejemplo, para N = 7:
El juego es muy simple. Se mezclan las cartas y se van sacando de a una. Si alguna carta sale en la posición que indica su número, pierde. Por ejemplo, si las cartas salen en el siguiente orden
podemos ver que es un juego perdido, dado que la carta con el número 5 ocupa el quinto lugar en la secuencia. En cambio, la siguiente secuencia es ganadora:
Apasionados por lo entretenido del juego, sus compañeros comienzan a hacer apuestas sobre si Francisco ganará o no la siguiente partida. "Te apuesto un desayuno en el comedor a que Francisco gana", le dice Lautaro a Rocío. Esta, criteriosa, prefiere hacer algunas cuentas antes de decidir si acepta o no la apuesta. Le gustaría conocer si la probabilidad de ganar es mayor a la de perder, para así saber si sería prudente aceptar.
Como Francisco juega con un mazo grande (N = 40), no es razonable analizar una por una todas las posibles ordenaciones del mazo para así saber la proporción exacta de "mazos ganadores" sobre el total.
Hay 815915283247897734345611269596115894272000000000 posibles permutaciones de un mazo de 40 cartas. Por otro lado, tratar de encontrar una fórmula exacta para el resultado es un problema combinatorio complicado. Para peor, se están terminando los desayunos en el comedor y hay que tomar una decisión en pocos minutos.
Por suerte para Rocío, ella recuerda que hay un método estadístico que la puede ayudar: El método de Montecarlo. A fin de cuentas, si se llama como un casino, algo de utilidad para juegos debe tener. "Si en pocos segundos yo pudiese jugar miles de veces a este juego, podría aproximar la probabilidad de ganar razonablemente", piensa. Sin más, pone manos en el teclado y escribe un programa que juega miles de partidas del Nada en su lugar, las clasifica en ganadoras o perdedoras, y calcula la proporción de ganadoras sobre el total. Obviamente, lo hace de forma tal que haya una constante N que represente la cantidad de cartas en el mazo, y que si cambiamos el valor de esta constante, obtenemos el resultado para un mazo de N cartas.
Ejercicio 6. Haga como Rocio y escriba su propio programa para este problema. ¿Le conviene o no aceptar la apuesta de Lautaro?
6 Algo de lógica proposicional
En la lógica clásica, una proposición es un enunciado al que, bajo ciertas reglas preestablecidas, es posible atribuirle un valor de verdad: verdadero o falso. Por ejemplo, "LCC es una carrera de tres años", "Las naranjas son frutas" y "Santa Fe tiene 19 departamentos" son ejemplos de proposiciones. A partir de proposiciones simples o atómicas se pueden construir proposiciones más complejas utilizando los conectivos lógicos. Por ejemplo, "Si Santa Fe tiene 19 departamentos, entonces las naranjas son frutas".
Los operadores lógicos más usados son la
conjunción (
),
la disyunción (
),
la negación (
),
la implicancia (
)
y la equivalencia (
).
Cuando trabajamos en lógica clásica, el significado de estos operadorados queda totalmente determinado a partir de su Tabla de verdad. Una tabla de verdad nos dice, para cada posible valor de verdad de las proposiciones más simples, cuál es el valor de verdad de la proposición. Ya vimos algunas tablas de verdad en la Práctica 0, tanto para la conjunción (and), disyunción (or) y negación (not). Las siguientes tablas de verdad se corresponden con la implicancia y la equivalencia:
p | q | (p |
#true | #true | #true |
#true | #false | #false |
#false | #true | #true |
#false | #false | #true |
p | q | (p |
#true | #true | #true |
#true | #false | #false |
#false | #true | #false |
#false | #false | #true |
Ejercicio 7. Para comenzar, se pide definir las funciones implica y equivalente, que dados
dos valores booleanos se comporten como la tabla de verdad de los operadores
y , respectivamente.
Cada fila de la tabla de verdad representa una valuación.
Esto es, una posible asignación de
valores de verdad para las variables involucradas en la fórmula.
Observemos que si una fórmula tiene n variables, entonces la tabla de verdad tendrá 
filas.
una tautología, si es verdadera para todas las posibles valuaciones;
una contradicción, si es falsa para todas las posibles valuaciones;
satisfactible, si es verdadera para al menos una valuación;
Consideremos las siguientes fórmulas proposicionales:
No es difícil observar que estas fórmulas son: una tautología, una fórmula satisfactible y una contradicción, respectivamente. Sin embargo, como todos sabemos, es mejor verlo a que te lo cuenten. Sería bueno que en este punto se detenga y haga con lápiz y papel la tabla de verdad de cada una de ellas.
Estamos interesados en diseñar los predicados tautología?, contradicción? y satisfactible?, que nos permitan clasificar fórmulas proposicionales. Haremos esto evaluando una fórmula en todas las posibles valuaciones. Es decir, el mismo método que siguen las tablas de verdad.
Para esto, deberíamos ser capaces de:
Poder representar valuaciones
Poder representar fórmulas proposicionales
Poder evaluar una fórmula en una valuación
6.1 Representando valuaciones
Para representar una valuación, podemos usar listas de booleanos. Por ejemplo, para la fórmula A, la lista (list #t #f #t) es una valuación posible. Si evaluamos la proposición en esta lista, obtenemos #t.
La lista (list #t #t) es una valuación posible para la fórmula C. Para esta valuación obtendremos #f como resultado.
Cada valuación representa una fila en la tabla de verdad de la proposición.
Ejercicio 8. Diseñe una función que, dado un número natural n, genere todas las posibles valuaciones que existen con n variables proposicionales. Por ejemplo, para n=3 debería devolver:
(list (list #false #false #false) (list #false #false #true) (list #false #true #false) (list #false #true #true) (list #true #false #false) (list #true #false #true) (list #true #true #false) (list #true #true #true))
6.2 Representando y evaluando fórmulas
La fórmula proposicional A puede pensarse como una función que, dados
tres valores booleanos a, b, c, devuelve el valor booleano que
resulta de sustituir 
por a, 
por b, y
por c.
Es decir, A podría representarse mediante una función de tres argumentos booleanos. Sin embargo, C debería representarse como una función de dos argumentos, puesto que sólo involucra dos variables proposicionales. Para hacer más uniforme la representación, utilizaremos listas de booleanos como argumentos de las fórmulas, y de esta manera podremos representar funciones proposicionales con cualquier cantidad de variables.
Usaremos la siguiente signatura para fórmulas:
List (Boolean) -> Boolean.
Con esta idea, podemos representar la fórmula A como sigue:
; A : List(Boolean) -> Boolean (define (A l) (equivalente (and (implica (first l) (third l)) (implica (second l) (third l))) (implica (or (first l) (second l)) (third l))))
; A : List(Boolean) -> Boolean (define (A l) (let ([p1 (first l)] [p2 (second l)] [p3 (third l)]) (equivalente (and (implica p1 p3) (implica p2 p3)) (implica (or p1 p2) p3))))
Las expresiones let nos permiten asociar uno o más nombres (por ejemplo, p1) a una o más expresiones (por ejemplo, (first l)). Para el ejemplo, los nombres p1, p2 y p3 sólo pueden usarse dentro de la definición de A.
Con esta definición, podemos evaluar:
(A (list #t #t #f)) > #t
Ejercicio 9. Defina las funciones B y C para las otras dos fórmulas que aparecen en los ejemplos. Obtenga el valor de verdad para cada una de ellas en un ejemplo concreto de valuación.
Ejercicio 10. Utilizando los ejercicios anteriores, defina una función evaluar que,
dada una fórmula proposicional P: List (Boolean) -> Boolean y la cantidad
de variables n que utiliza P, devuelva una lista con
booleanos, que son el resultado de evaluar P
en cada una de las posibles valuaciones. Es decir, que devuelva una lista con la última columna de
la tabla de verdad de P.
Ejercicio 11. Diseñe los predicados tautología?, contradicción? y satisfactible?.