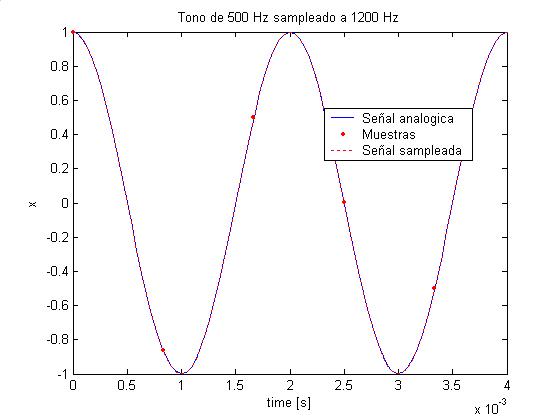
f = 500 Hz
Fs = 1200 Hz
Audio de la señal analógica
Audio de la señal reconstruida a través de muestras
Tono Puro
Consideramos una señal analógica dada por un tono puro
x(t) = sin( 2 p f t ) ,
cuya frecuencia es f .
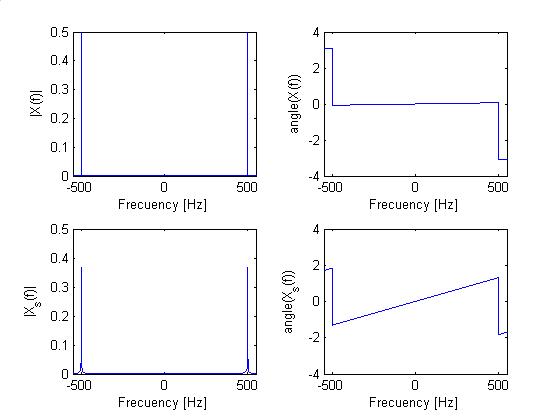
Sabemos a través el Teorema de Muestreo que si muestreamos a una frecuencia Fs > 2 f no hay aliasing y además es posible reconstruir la señal analógica a través de sus muestras. Aliasing aparece si muestreamos a Fs < 2 f . Esto puede verse en las siguientes gráficas.
Caso a: Fs > 2 f
|
|
f = 500 Hz Fs = 1200 Hz |
|
|---|---|---|
|
|
||
|
Audio de la señal analógica |
||
|
Audio de la señal reconstruida a través de muestras |
||
|
|
||
|
|
|
|
Caso b: Fs = 2 f
|
|
f = 500 Hz Fs = 1000 Hz |
|
|---|---|---|
|
|
||
|
Audio de la señal analógica |
||
|
Audio de la señal reconstruida a través de muestras |
||
|
|
||
|
|
|
|
Caso c: Fs < 2 f
|
|
f = 500 Hz Fs = 800 Hz |
|
|---|---|---|
|
|
||
|
Audio de la señal analógica |
||
|
Audio de la señal reconstruida a través de muestras |
||
|
|
||
|
|
|
|