Al finalizar el Trabajo Práctico usted debería ser capaz de:
- Diseñar filtros FIR de fase lineal usando el método de muestreo en frecuencia (frequency sampling), implementando el algoritmo de cómputo en Matlab, y usando la función fir2.
- Diseñar filtros FIR de fase lineal usando el método de enventanado (windowing), y su implementación en Matlab (función fir1).
- Diseñar filtros FIR de fase lineal usando el método de mínimos cuadrados, y su implementación en Matlab (función firls).
- Diseñar filtros IIR a partir de filtros analógicos, mediante Transformación Bilineal.
- Diseñar filtros FIR de fase lineal y filtros IIR a partir de especificaciones de la respuesta en frecuencia, usando la herramienta de Matlab fdatool.
- Implementar filtros FIR e IIR en tiempo real, usando el TMS320C6713 DSP Starter Kit (DSK).
- Filtrado usando Matlab
- Diseño de filtros FIR de fase lineal
- Determine y grafique los coeficientes h(n) de un filtro FIR de fase
lineal pasabajos de
longitud M=15 , que tenga una respuesta al impulso unitario simétrica, y
una respuesta en frecuencia que satisfaga la condición
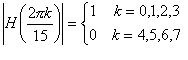
- Repita el diseño del filtro del item anterior pero para la
siguiente especificación de respuesta en frecuencia
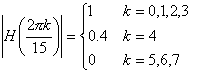
- Determine los coeficientes h(n) de un filtro FIR pasabajo de fase lineal de longitud M=15 , que tenga una respuesta al impulso unitario simétrica, y una frecuencia de corte igual a 0.2 Fs, siendo Fs la frecuencia de muestreo. Utilice para el diseño la función fir1 de Matlab, empleando diferentes ventanas. Compare las diferentes respuestas en frecuencia obtenidas.
- Repita el problema 2., pero usando la función fir2 de Matlab. Compare la respuesta en frecuencia obtenida con la correspondiente al problema 2. Utilice diferentes ventanas y compare las distintas respuestas en frecuencia obtenidas.
- Repita el problema 2., pero usando la función firls de Matlab. Compare la respuesta en frecuencia obtenida con la correspondiente al problema 2.
- Aplicación: Filtrado de una señal de audio
- El archivo handel.m de Matlab contiene una señal de audio que
corresponde a los primeros 4 compases de coro del "Hallellujah Chorus" del Oratorio
"Messiah" de G. F. Handel (1685-1759). La señal de audio puede cargarse en el
espacio de trabajo de Matlab mediante el comando
>> load handel - Genere un tono puro con la nota Mi (frecuencia fMi = 440 x 27/12 Hz) y la misma duración que la señal en handel.m, y adiciónelo a la señal. Considere una amplitud igual a 0.5.
- Visualice el espectro de la señal con ruido.
- Diseñe un filtro FIR elimina-banda, de fase lineal y de orden mínimo, que elimine (atenúe) las frecuencias comprendidas entre las notas Re# (frecuencia fRe# = 440 x 26/12 Hz) y Fa (frecuencia fFa = 440 x 28/12 Hz). El rizado máximo de las bandas de paso debe ser 1 dB, en tanto que la atenuación mínima de la banda de rechazo debe ser 60 dB. Puede hacer uso de la herramienta fdatool de Matlab para el diseño.
- Grafique la respuesta en frecuencia del filtro, su respuesta al impulso, y el diagrama de polos y ceros.
- Filtre la señal con ruido y visualice el espectro de la señal filtrada junto con el de la señal con ruido. Escuche la señal filtrada y verifique que el tono (ruido tonal) ha sido suficientemente atenuado de manera que resulta imperceptible.
- El archivo handel.m de Matlab contiene una señal de audio que
corresponde a los primeros 4 compases de coro del "Hallellujah Chorus" del Oratorio
"Messiah" de G. F. Handel (1685-1759). La señal de audio puede cargarse en el
espacio de trabajo de Matlab mediante el comando
- Determine y grafique los coeficientes h(n) de un filtro FIR de fase
lineal pasabajos de
longitud M=15 , que tenga una respuesta al impulso unitario simétrica, y
una respuesta en frecuencia que satisfaga la condición
- Diseño de filtros IIR
- Use el método de la Transformación Bilineal para hallar la función
transferencia de un filtro IIR en tiempo discreto que corresponda a un filtro
pasabajo del tipo Chebychev de segundo orden, con r=1.5 dB factor de rizado en la banda
de paso, una ganancia máxima igual a 1, y una frecuencia de corte de
fc = 30 Hz . Use
una frecuencia de muestreo de fs = 200 Hz . Compare las
respuestas en frecuencia de
los filtros discreto y continuo, graficando sus módulos en una misma figura.
Para el diseño, considere los siguientes dos casos:
- Transformación Bilineal para "matching" exacto a frecuencia cero.
- Transformación Bilineal para "matching" exacto a la frecuencia de corte.
- La función transferencia de un filtro Chebychev de
segundo orden viene dada por
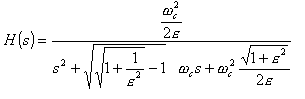
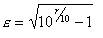
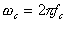es la pulsación de corte. -
La transferencia discreta usando la Transformacion Bilineal viene dada por
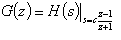
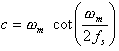
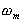la pulsación de
"matching".
- Repite el problema anterior, pero usando ahora la función Matlab cheby1 para generar el filtro analógico. Compare los resultados obtenidos con los del problema anterior.
- Utilice la función Matlab cheby1 para diseñar en forma directa un filtro digital que sea equivalente al del problema 1.
- Utilice la función Matlab lp2hp para diseñar un filtro pasa alto complementario al del problema anterior.
- Repita el problema I.a.6, pero diseñando ahora un filtro IIR elimina-banda, de Chevyshev, de orden mínimo.
- Use el método de la Transformación Bilineal para hallar la función
transferencia de un filtro IIR en tiempo discreto que corresponda a un filtro
pasabajo del tipo Chebychev de segundo orden, con r=1.5 dB factor de rizado en la banda
de paso, una ganancia máxima igual a 1, y una frecuencia de corte de
fc = 30 Hz . Use
una frecuencia de muestreo de fs = 200 Hz . Compare las
respuestas en frecuencia de
los filtros discreto y continuo, graficando sus módulos en una misma figura.
Para el diseño, considere los siguientes dos casos:
- Diseño de filtros FIR de fase lineal
- Implemente en el DSP Kit el filtro FIR diseñado en el punto I.a.6. Verifique su correcto funcionamiento capturando la salida (señal filtrada) y analizando su espectro.
- Implemente en el DSP Kit el filtro IIR diseñado en el punto I.b.5. Verifique su correcto funcionamiento capturando la salida (señal filtrada) y analizando su espectro.