Determinar los extremos relativos de

 f(x,y) = 1 - (x ² + y ²) ^1/3

 Evidentemente, esta función tiene un único extremo que es un máximo relativo en (0, 0) pues

       0 ≤ (x ² + y ²) ^1/3                 

 ^{Dicho extremo también es absoluto}

 Para resolver el problema  se calculan  las derivadas parciales

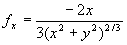
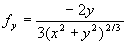
  Ambas derivadas parciales están definidas en todo el plano x y, salvo en el origen. 

 Siendo  f(0,0) = 1, se puede  deducir de la ley de f que, para cualquier otro punto es  f(x,y) < 1.

 Luego f(0,0) es un máximo relativo.
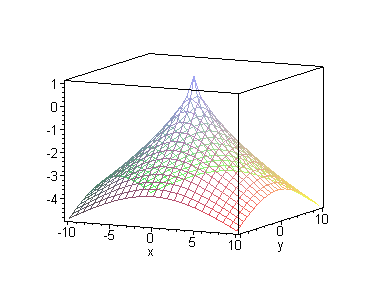